Adaptive spectral panning

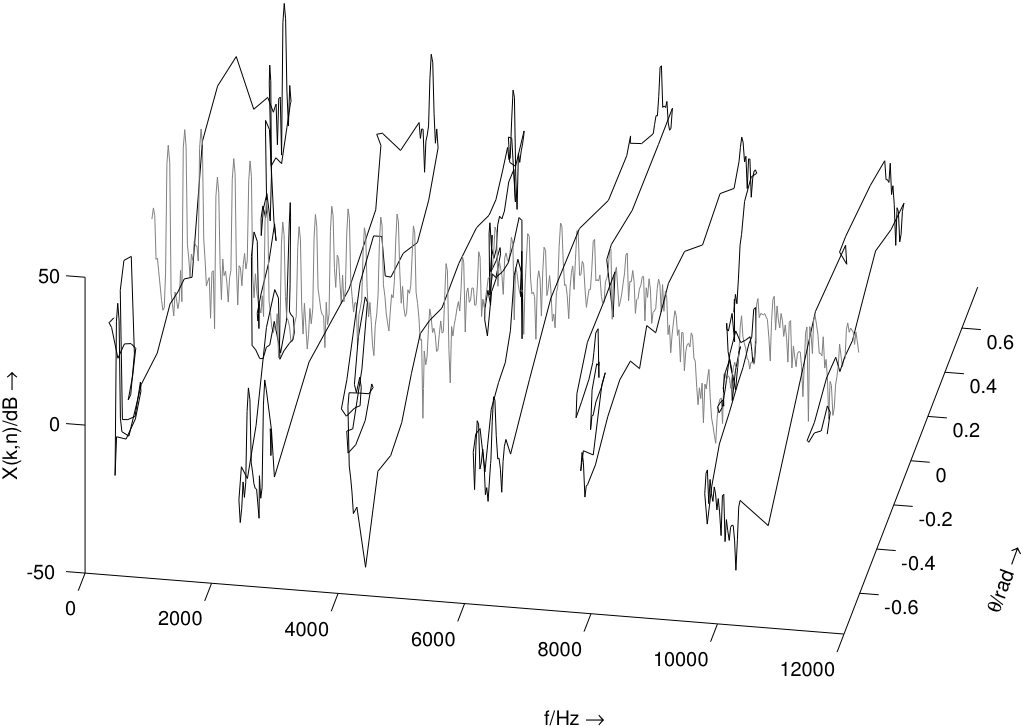
The spectral panning effect consists in converting a mono sound signal into a stereo sound signal where each frequency component is placed to its own azimuth position between the loudspeakers, creating an spectral split effect. One implementation is based on the short-term Fourier transform, and replaces a single spectrum (mono signal) by two spectra, while preserving the signal power with Blumlein's constant-power pan law. In its adaptive version, spectral panning uses a vector sound descriptors (such as the spectral envelope, the spectrum itself, the waveform, etc) to control the panning angle of each frequency bin.

Implementation details
The technique proposed here relies on the short-term Fourier transform, with its overlap-add process. For each input windowed-grain (at time t= m RA), the input spectrum X[m,k] is computed with the FFT. Two spectra Yl[mk,k] and Yr[m,k] are then generated:
- their phases have the same value as the input spectrum (dirty trick, to limit Doppler effect, but resulting in inter-aural time and intensity differences)
- their magnitudes are derived from the multiplication of the input magnitude spectrum and the spectral-panning curve using the Blumlein panning law (for loudspeakers with a 90 angle), that ensures a constant-power:
Yl[m,k] = sqrt(2)/2 . [ cos(theta[m,k]) + sin(theta[m,k]) ] . X[m,k]
Yr[m,k] = sqrt(2)/2 . [ cos(theta[m,k]) - sin(theta[m,k]) ] . X[m,k]

The process is then repeated with the overlap-add technique, if possible with a time increment RA smaller or equal to the window size N:
RA

Control parameters

• gamma[m] in [0,1]: the maximum amount of panning
• C[m,k] in [-pi/2, pi/2]: the spectral panning curve (same size N as the FFT)
• Fc in Hz: the low-pass filter frequency of the control curve
• RA in samples: time increment between windows (constant)
• N in samples: window size (constant)

From gamma[µ] and C[m,k], we derive the panning angle vector depending on the wanted mapping, for instance as:
theta[m,k] = gamma[m] . C[m,k]

To avoid artifacts, the panning angle of each frequency bin should not change faster than 20 Hz, where amplitude modulations start to be heard heard in the spectral domain. Therefore, some time-smoothing (or low-ass filtering) is needed. This can be obtained by computing the spectral panning curve as a slow interpolation between two successive values of the vector sound descriptors at key frames, which indexes are denoted m1 and m2.
Let us denote Fs the sound sampling frequency, and Tc the time increment for the sub-sampled control (with Fc = Fs / T). Then, for m2 - Tc
alpha[m] = (m - m2) / Tc
 C[m,k] = alpha[m] . C[m1,k] + (a-alpha[m]) . C[m2,k]

A simple choice for m1 is m1 = m2 - Tc.

Perceptual viewpoints
The following attributes are modified:

• panning

The following attributes are note supposed to be modified:

• loudness
• duration
• pitch (except if Fx >= 20 Hz)

The following attributes are only modified if Fc >= 20 Hz:

• pitch, timbre (inharmonicity) due to ring modulation if Fc >= 20 Hz
• loudness and timbre (roughness) if Fc >= 10 Hz

Flowchart diagram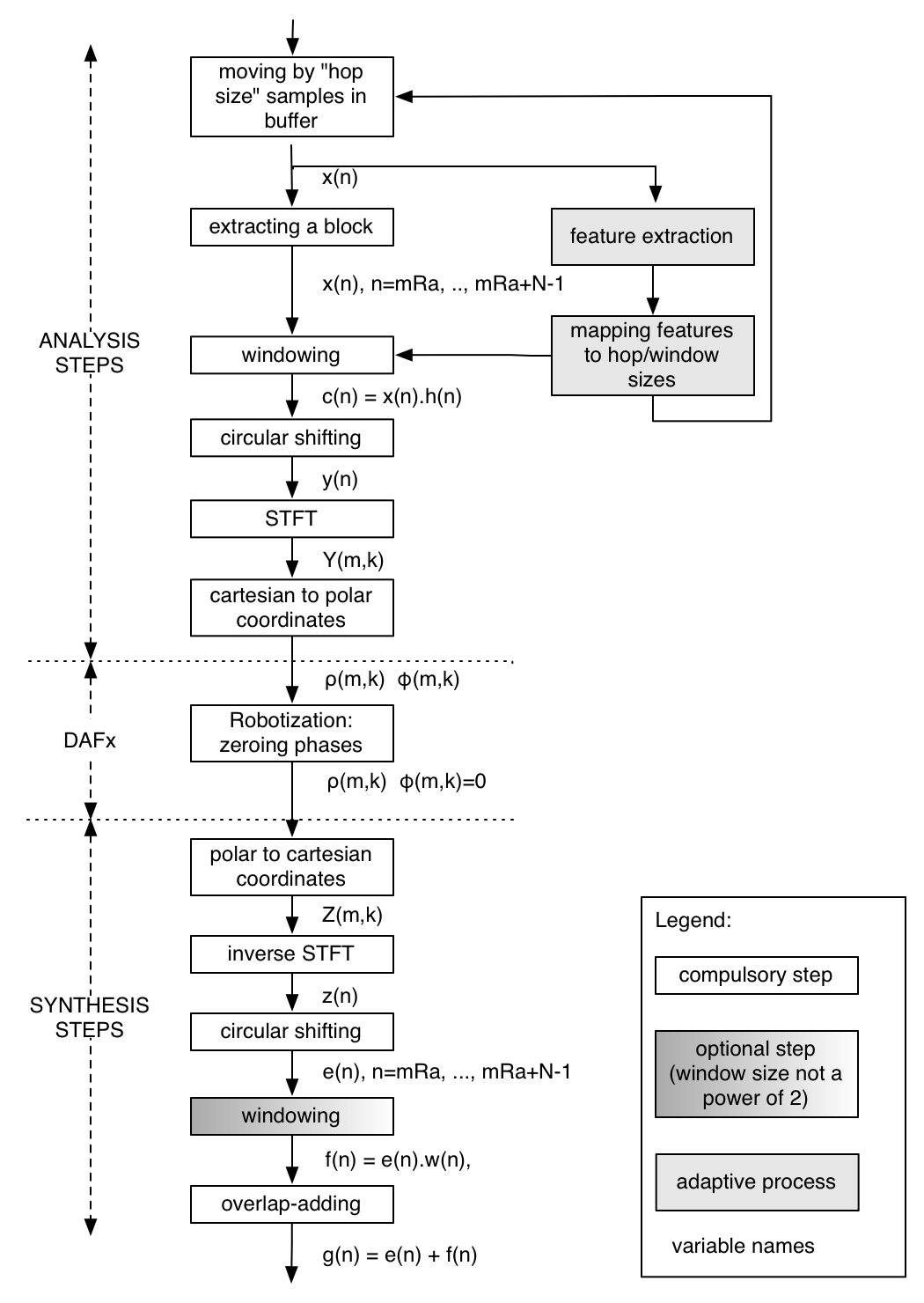

Bibliography

• V. Verfaille, U. Zölzer and D. Arfib, "Adaptive Digital Audio Effects (A-DAFx): A New Class Of Sound Transformations". In IEEE Transactions on Acoustics Speech and Language Processing, pages 1817-1831. Vol 14, number 5, 2006.